En el presente artículo vamos a ver un rápido y sencillo para realizar operaciones con matrices. Para lo cual haremos uso del módulo "numpy" el cual, nos permite realizar operaciones de forma sencilla y eficiente sobre grandes conjuntos de información que puede organizarse en vectores.
Puesto que vamos a trabajar con "numpy", si lo tenemos ya instalado, lo primero que haremos será importarlo. En caso de que no lo tengamos aún instalado tendremos que hacer uso de "pip" para su instalación:

Importación de "numpy" como "np":

Para crear matrices, tenemos que crear primero la matriz con las dimensiones deseadas, para luego asignarles los valores mediante un ciclo "for". Con "numpy" solo tendremos que crear dos arrays con tantos vectores como filas queramos que tenga nuestra matriz (a su vez, cada uno de esos vectores tendrá tantos elementos como columnas queramos que tenga la matriz) y especificando, al final, el formato que queremos aplicar a los elementos del array ("float" en este caso). Así empezaremos creando la primera matriz (a la que daremos el nombre de "matriz_1"):

Hecho esto (tal y como se aprecia en la imagen) hemos creado la primera de las matrices que vamos a sumar. Para la creación y visualización de la segunda matriz (que llevará por nombre "matriz_2") empelearemos el mismo procedimiento:

Una vez que tenemos creadas las dos matrices podremos realizar sencillas operaciones con ellas. Como es el caso de la suma y la resta (operaciones las cuales hemos llevado a cabo en nuestro ejemplo mediante los operadores "+" y "-"):

Para el caso de la multiplicación de matrices, en su momento, vimos como dicho proceso era algo , más complejo que el de la suma/resta. Sin embargo, en "numpy" contamos con una función especifica para la multiplicación de matrices (la función "np.dot"), mediante la cual, una ves creadas las dos matrices a multiplicar, nos permite llevar a cabo dicha operación de un modo sencillo tal y como se puede apreciar en la imagen:

Visto el modo sencillo con el que podemos efectuar operaciones con matrices, nos proponemos, ahora, a crear un programa (cuyo código completo podéis ver en el enlace que dejo al final) que nos permite realizar sencillas operaciones de suma y resta de matrices, mediante la introducción de estas seguidas de un operador ("+" o "-") que indique la operación a realizar.

Tras ello, mostraremos en pantalla una tabla de operadores en la que se nos muestra las operaciones que podrá efectuar nuestra calculadora y los inputs a introducir para ello:
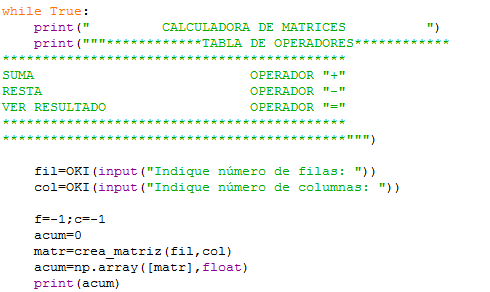
A continuación crearemos dos variables, "fil" y "col" que representarán el número de filas y columnas, respectivamente, de las que va a constar las matrices que vamos a crear para realizar la operación (debido a que para sumar y restar matrices es necesario que estas tengan las mismas dimensiones, nuestras variables "fil" y "col" valdrán para todas las matrices que vayamos creando).
A su vez puesto que queremos que el input para "fil" y "col" sea un número entero, usaremos la función "OKI" para asegurarnos de que el usuario solo pueda introducir in dato de tal naturaleza:

A su vez, dado que para efectuar los cálculos vamos a tener que ir creando las matrices con las que trabajar, definiremos una función a la que llamaremos "crea_matriz", la cual, tomando como argumentos los valores de "fil" y "col", establecidos con anterioridad, hará uso de dos ciclos "for" (uno que recorrerá el rango entre 0 y el número de filas y, para cada elemento de "filas", otro que recorra el rango entre 0 y el número de columnas) para ir realizando la asignación de los distintos valores de la matriz. A su vez, los componentes "x" e "y" de la matriz serán representados por las variables "f" y "c", ambas con valor inicial igual a -1:

Para la introducción del valor para cada elemento de la matriz, emplearemos la función "OK" para asegurarnos de que solo se introduzca un valor numérico:

La función "crea-matriz", nos devolverá una lista de vectores ("e_fil") que son los que a continuación emplearemos para crear el array que usaremos en el calculo con "np.array" y que se guardará en la variable "acum". Puesto que queremos que la matriz creada se muestre tras su creación, usaremos "print(acum)" para mostrarla:

Tras la creación de cada matriz, usaremos una variable (a la que llamaremos "oper") mediante la que pediremos la operación que quiere el usuario realizar con la matriz. Dicho valor de "oper" será "+" para sumar, "-" para restar y "=" para mostrar la matriz resultado. Un ejemplo de ejecución de lo que estamos diciendo sería el siguiente:

Este procedimiento de creación de matrices/introducción de operación a realizar, se repetirá dentro de un ciclo "while" el cual solo se romperá una vez que el usuario introduzca "=" en el input para la variable "oper" (lo que también llevará a que se muestre la "matriz resultado":

Finalmente daremos la posibilidad de reanudar el programa preguntándole a nuestro usuario si quiere llevar a cabo tal acción, mediante el correspondiente input para "conti" a lo que el usuario tendrá que contestar solo "n" (para "no") o "s" (para "si"):

Para asegurarnos de que solo se introduce una de dichas respuestas ("n" o "s") usaremos la función "ns" que se aplicará sobre la respuesta dada por el usuario:

De ese modo, si el usuario introduce "n" el programa finalizará y si introduce "s" se hará una limpieza de consola (mediante "subprocess") dejando el programa listo para una nueva ejecución.
El código completo de nuestra calculadora de matrices puede consultarse en el siguiente enlace a Github:
https://github.com/antonioam82/calculadora-de-matrices
Saludos.
Comentarios
Publicar un comentario