Expresiones Regulares con Python - Ejemplos Prácticos

¿Qué son las Expresiones Regulares?

Las expresiones regulares, son una secuencia de caracteres que forma un patrón de búsqueda. Los patrones se interpretan como un conjunto de instrucciones que luego se ejecutan sobre un texto de entrada para producir una versión modifica del texto original. Las expresiones regulares pueden incluir patrones de coincidencia literal, de repetición, de composición, de ramificación, y otras sofisticadas reglas de reconocimiento de texto.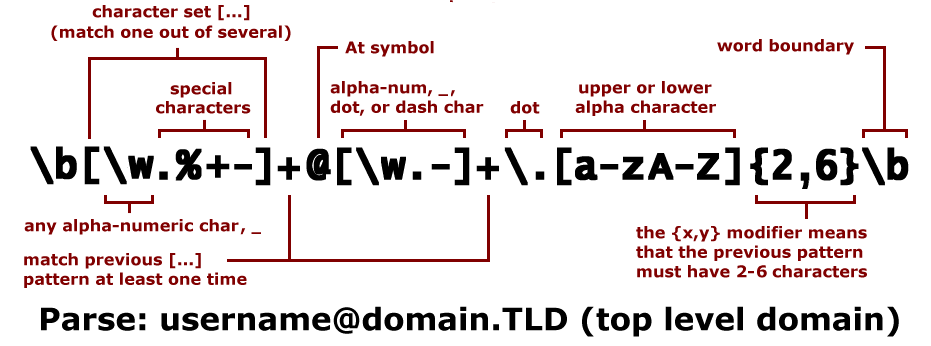

Expresiones Regulares - Ejemplos Prácticos:

Muy bien, ya sabemos que las expresiones nos sirven para trabajar y procesar cadenas de textos. Las expresiones regulares son usadas para distintos propósitos: direcciones de paginas web, reconocimiento de correos electrónicos, búsqueda de coincidencias en textos, entre otros.

Muy bien, es hora de probar las expresiones regulares con código Python.

El lenguaje de programación, en su librería estándar, nos proporciona el modulo regex el cual es utilizado para trabajar con expresiones regulares.

import re # Importamos el modulo regex

# El metodo mathc determina si la expresión regular tienen coincidencias
# en el comienzo del texto

def coincidencias(text1, text2):
    if re.match(text1, text2):
        return True
    else:
        return False
    
coincidencias("Python", "Python")

True

# Con expresiones regulares, podremos buscar todo tipo de patrones
# Por ejemplo, podremos iltrar las palabras con acentos
patron = ('\w*[ñáéíóúÑÁÉÍÓÚ]\w*')
palabras = re.compile(patron)
palabras.findall("Niño, Acción, Perro, Lobo, Expresión, Español")

['Niño', 'Acción', 'Expresión', 'Español']

# Podemos utilizar las expresiones regulares para la validación de URL

#Este serie el patron que sigue una URL
url = re.compile(r"^(https?:\/\/)?([\da-z\.-]+)\.([a-z\.]{2,6})([\/\w \.-]*)*\/?$")

if url.search("http://pythondiario.com/"): # Comprobemos que esta es una URL valida
    print("URL Valida")
else:
    print("URL No Valida")

URL Valida

# Uno de los usos que más se le dan a las expresiones regulares
# es la verificación de correos electronicos
patron = re.compile(r"[\w.%+-]+@[\w.-]+\.[a-zA-Z]{2,6}")

if patron.search("pythondi1io@gmail.com"): # Comprobemos sí este es un correo electronico valido
    print("Correo valido!")
else:
    print("Correo Invalido!")

Correo valido!

Con las expresiones regulares también podemos verificar una fecha. A continuación les mostrare un ejemplo:

fecha = re.compile(r'^(0?[1-9]|[12][0-9]|3[01])/(0?[1-9]|1[012])/((19|20)\d\d)$')

if fecha.search("13/02/1982"):
    print("Fecha Valida!")
else:
    print("Fecha Invalida!")

Fecha Valida!

if fecha.search("332/49/1982"):
    print("Fecha Valida!")
else:
    print("Fecha Invalida!")

Fecha Invalida!

¿Alguna duda? No olvides dejar tu comentario.

¿Con ganas de más? Ingresa al siguiente enlace el cual te redirigirá a un buen libro sobre Python, desde lo más básico hasta lo más avanzado: Python Para Todos PDF Español.

Puedes descargar todos los ejemplos realizados en este articulo Ingresando Aquí.