Sistema Hexadecimal - Sistema de numeración posicional

Sistema Hexadecimal

El sistema hexadecimal es un sistema numérico que tiene como base el numero 16, y es una variante de los numero binarios

El sistema hexadecimal es utilizado por nuestros ordenadores con el fin de abreviar valores de datos e instrucciones de memoria.

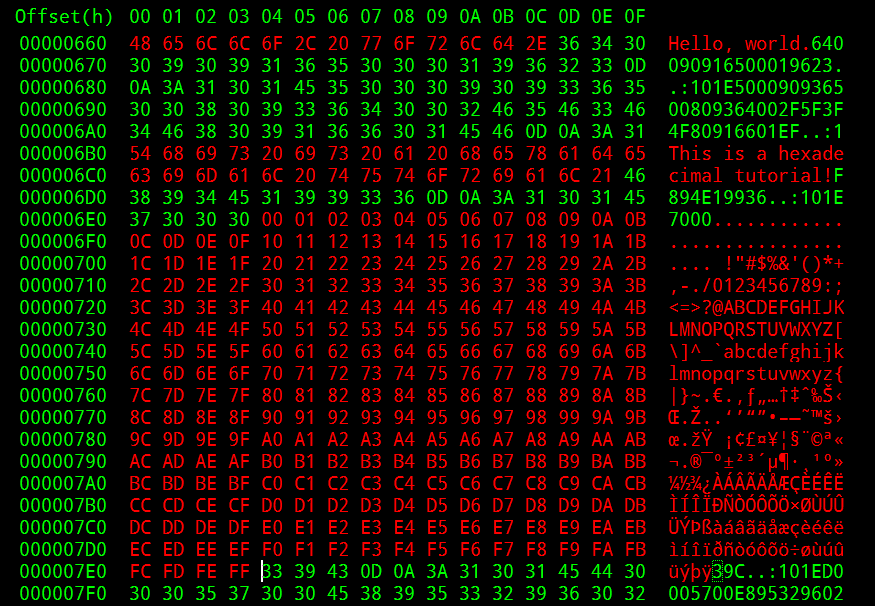
Esta es una imagen que muestra el contenido de un archivo con exención 'dll' en un editor de texto, como el editor de texto no reconoce este tipo de archivo, nos lo muestra de esta manera:

Como se puede apreciar, en vez de ver una gran cantidad de 0 y 1, vemos que hay grupos de 4 dígitos, y si observamos, vemos que son grupos de dígitos hexadecimales. El archivo cuentan con más de 48 mil lineas, por ello no se me es posible mostrarlo todo. Este es uno de los usos del sistema hexadecimal para abreviar grandes cantidades de 0 y 1. Ustedes mismos pueden hacer la prueba con una imagen o con cualquier otro tipo de texto.

El sistema hexadecima, esta conformado por solo 16 dígitos. A continuación te los presento:

Representación de la base 16.

Como mencione anteriormente, la base del sistema hexadecimal es 16, por ello cuenta con solo 16 caracteres (10 números y 6 letras). Como se puede apreciar en la tabla de arriba, el sistema hexadecimal cuenta con 10 numero que van del 0 - 9 y con 6 letras, las cuales son las primeras 6 letras de abecedario (A, B, C, D, E, F). En la tabla pueden observar que A es equivalente a 10, que B es equivalente a 11 y así sucesivamente. Creo que me explique bien ¿No?.

El sistema hexodeccimal es utilizado por microordenadores porque  es un método adecuado para acortar largas series de unos y ceros (numero binarios). Cada grupo de bits se puede convertir en un valor hexadecimal (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F), como se muestra en la siguiente tabla.


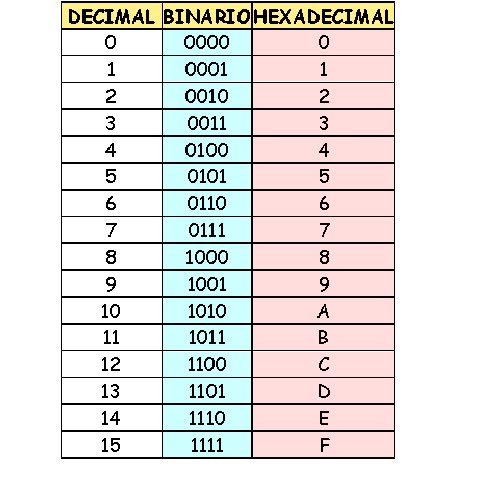
Esta tabla se parece a la primera, simplemente que en esta se puede apreciar los equivalente de binario a decimal y a hexadecimal.

Pasar de binario a hexadecimal es algo muy simple. Empezando por el bit de la derecha, dividimos el número binario en grupos de cuatro. Si no tenemos un múltiplo entero de cuatro (4, 8, 12, etc.), quedan algunos bits vacíos a la izquierda; en este caso, se debe rellenar a ceros sin más. Después, convertimos cada grupo de cuatro bits en un dígito hexadecimal. El resultado es la representación hexadecimal del valor binario, que es la cuarta parte de largo en caracteres.

Para entender mejor el procedimiento, realicemos un ejemplo:

Supongamos que tenemos el siguiente numero binario de 16 bits:

1101001111000101

Como nos indica el procedimiento, debemos dividir esta secuencia en grupos de cuatro bits. Nos debería quedar algo así:

1101 - 0011 - 1100 - 0101

Ahora, pasamos cada grupo a un dígito hexadecimal. Nos podemos guiar por la tabla que les presente anteriormente la cual nos dice que "1101" en hexadecimal es equivalente a "13", "0011" en hexadecimal es equivalente a "3", "1100" en hexadecimal es equivalente a "12" y que "0101" en hexadecimal es equivalente a "A". Nos debería quedar algo así:

1101 - 0011 - 1100 - 0101 = 13 3 12 A

De esta manera, abreviamos la secuencia de 16 bits:

1101001111000101

A:

1331A

Para pasar de hexadecimal a binario, debemos invertir el procedimiento. Tomamos cada dígito hexadecimal y lo convertimos en un grupo de cuatro bits. Realicemos otros ejemplo.

Tenemos la siguiente secuencia hexadecimal:

5F7A

Lo que hacemos, es traducir dígito por dígito. 5 en binario es "0101", F (15) en binario es "1111", 7 en binario es "0111" y A (10) en binario es "1010". Nos debería quedar algo así:

5F7A =  0101111101111010

Y de esta manera, obtenemos como resultado una secuencia de 16 bits.


Python nos proporciona métodos y bibliotecas nativas que nos permiten trabajar con distintos sistemas numéricos (hexadecimal, octal, entre otros). En este blog ya hemos tratado con bibliotecas para el manejo de sistemas numéricos (http://www.pythondiario.com/2017/12/codificacion-de-datos-con-base64.html).

Python también nos proporciona el método "int" (usado para la conversión de datos) al cual le podemos pasar 2 argumentos: 1- La secuencia. 2- Base del sistema numerico.

A continuación les mostrare un ejemplo usando el método "int". Lo usare para pasar "A5F2" a su forma decimal.

int('A5F2', 16) # 16 es base usada por el sistema hexadecimal

Out[1]:

42482

int('5F7A', 16)

Out[2]:

24442

int('13312A', 16)

Out[3]:

1257770

Esos fueron unos ejemplos sencillo para decodificar cadenas hexadecimales a su forma decimal. 

Con el modelo base64, podemos codificar y decodificar datos a distintos tipos de sistemas numéricos. A continuación te mostrare un ejemplo, el cual codifica una cadena de texto ('Dato').

import base64 # Importamos la libreria base64

hexadecimal = base64.b16encode(b'Dato') # Codificamos la cadena 'Dato'
print(hexadecimal) # Mostramos el resultado

b'4461746F'

Como pueden observar, el resultado es una secuencia de dígitos en hexadecimal. Si se fijan, la cadena de texto ('Dato') la hemos pasado a binario, de esta manera se podrá codificar como el procedimiento que hemos visto anteriormente. El resultado es la forma hexadecimal de 'Dato'.

Muy bien, pero ahora, quiero pasar de decimal a hexadecimal. Para ello, podemos escribir nuestro propio programa que sea capaz de lograr este objetivo. A continuación te mostrare un pequeño scripts que toma los decimales que se les de como entrada y los transforma a hexadecimal. A continuación te mostrare el código:

def DecimalAHexodecimal(): # Esta sera nuestra función principal
    decimal = int(input("Introduzca un numero positivo para convertirlo a hexodecimal: ")) # Pedimos los decimales al usuario
    hexadecimal = "" # En esta variable almacenaremos el valor hexodecimal
    while decimal != 0: 
        # Cambiamos los digitos por los hexodecimales
        rem = CambiarDigitos(decimal % 16)
        # Llenamos la varibale "hexodecimal" con los nuevos valores
        hexadecimal = str(rem) + hexadecimal
        decimal = int(decimal / 16)
    print("Resultado: " + hexadecimal) # Mostramos el resultado

def CambiarDigitos(digitos): # Esta funcion traduce los digitos a sus respectivos hexodecimales
    decimales =     [10 , 11 , 12 , 13 , 14 , 15 ]
    hexadecimal = ["A", "B", "C", "D", "E", "F"]
    for c in range(7):
        if digitos == decimales[c - 1]:
            digitos = hexadecimal[c - 1]
    return digitos

DecimalAHexodecimal()

Introduzca un numero positivo para convertirlo a hexodecimal: 95
Resultado: 5F

Al ejecutar el programa, nos pedirá el numero decimal que queremos pasar a hexadecimal. En mi caso introduje el numero 95, el cual me da como resultado '5F'. De esta manera sabemos que '5F' es 95.

Descarga el código de muestra Ingresando Aquí.  


Bueno, eso es todo por hoy. Esto es información, que cualquiera en el mundo de la informática debería de conocer.

Comparte tu experiencia con nosotros dejando un buen comentario.